bamlss: Bayesian Additive Models for Location, Scale, and Shape (and beyond) pdf
N. Umlauf, N. Klein, T. Simon and A. ZeileisJournal of Statistical Software, 100(4), 1–53, 2021

See the Google Scholar page of Prof. Klein for a complete and up-to-date list, below some key publications are listed. For a complete list of publications, please refer to the following subpages:
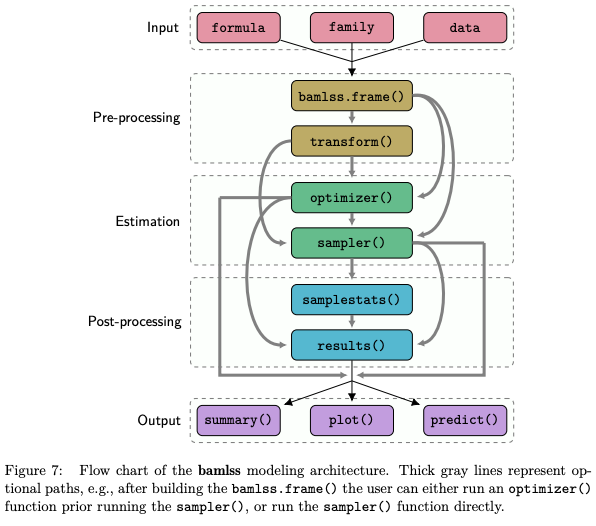
Abstract: Over the last decades, the challenges in applied regression and in predictive modeling have been changing considerably: (1) More flexible regression model specifications are needed as data sizes and available information are steadily increasing, consequently demanding for more powerful computing infrastructure. (2) Full probabilistic models by means of distributional regression - rather than predicting only some underlying individual quantities from the distributions such as means or expectations - is crucial in many applications. (3) Availability of Bayesian inference has gained in importance both as an appealing framework for regularizing or penalizing complex models and estimation therein as well as a natural alternative to classical frequentist inference. However, while there has been a lot of research on all three challenges and the development of corresponding software packages, a modular software implementation that allows to easily combine all three aspects has not yet been available for the general framework of distributional regression. To fill this gap, the R package bamlss is introduced for Bayesian additive models for location, scale, and shape (and beyond) - with the name reflecting the most important distributional quantities (among others) that can be modeled with the software. At the core of the package are algorithms for highly-efficient Bayesian estimation and inference that can be applied to generalized additive models or generalized additive models for location, scale, and shape, or more general distributional regression models. However, its building blocks are designed as "Lego bricks" encompassing various distributions (exponential family, Cox, joint models, etc.), regression terms (linear, splines, random effects, tensor products, spatial fields, etc.), and estimators (MCMC, backfitting, gradient boosting, lasso, etc.). It is demonstrated how these can be easily combined to make classical models more flexible or to create new custom models for specific modeling challenges.
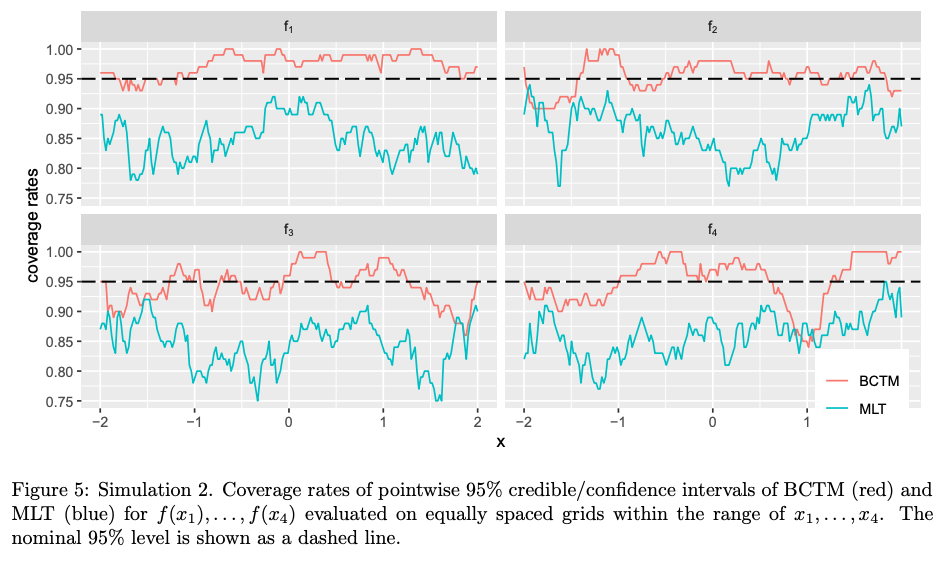
Abstract: Recent developments in statistical regression methodology shift away from pure mean regression toward distributional regression models. One important strand thereof is that of conditional transformation models (CTMs). CTMs infer the entire conditional distribution directly by applying a transformation function to the response conditionally on a set of covariates toward a simple log-concave reference distribution. Thereby, CTMs allow not only variance, kurtosis or skewness but the complete conditional distribution to depend on the explanatory variables. We propose a Bayesian notion of conditional transformation models (BCTMs) focusing on exactly observed continuous responses, but also incorporating extensions to randomly censored and discrete responses. Rather than relying on Bernstein polynomials that have been considered in likelihood-based CTMs, we implement a spline-based parameterization for monotonic effects that are supplemented with smoothness priors. Furthermore, we are able to benefit from the Bayesian paradigm via easily obtainable credible intervals and other quantities without relying on large sample approximations. A simulation study demonstrates the competitiveness of our approach against its likelihood-based counterpart but also Bayesian additive models of location, scale and shape and Bayesian quantile regression. Two applications illustrate the versatility of BCTMs in problems involving real world data, again including the comparison with various types of competitors. Supplementary materials for this article are available online.
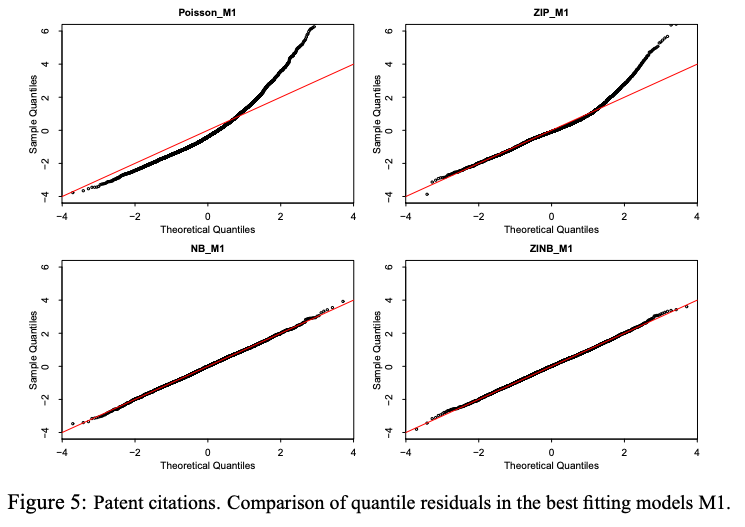
Abstract: Frequent problems in applied research preventing the application of the classical Poisson log-linear model for analyzing count data include overdispersion, an excess of zeros compared to the Poisson distribution, correlated responses, as well as complex predictor structures comprising nonlinear effects of continuous covariates, interactions or spatial effects. We propose a general class of Bayesian generalized additive models for zero-inflated and overdispersed count data within the framework of generalized additive models for location, scale, and shape where semiparametric predictors can be specified for several parameters of a count data distribution. As standard options for applied work we consider the zero-inflated Poisson, the negative binomial and the zero-inflated negative binomial distribution. The additive predictor specifications rely on basis function approximations for the different types of effects in combination with Gaussian smoothness priors. We develop Bayesian inference based on Markov chain Monte Carlo simulation techniques where suitable proposal densities are constructed based on iteratively weighted least squares approximations to the full conditionals. To ensure practicability of the inference, we consider theoretical properties like the involved question whether the joint posterior is proper. The proposed approach is evaluated in simulation studies and applied to count data arising from patent citations and claim frequencies in car insurances. For the comparison of models with respect to the distribution, we consider quantile residuals as an effective graphical device and scoring rules that allow us to quantify the predictive ability of the models. The deviance information criterion is used to select appropriate predictor specifications once a response distribution has been chosen. Supplementary materials for this article are available online.
Abstract: We propose a new semi-parametric distributional regression smoother that is based on a copula decomposition of the joint distribution of the vector of response values. The copula is high-dimensional and constructed by inversion of a pseudo regression, where the conditional mean and variance are semi-parametric functions of covariates modeled using regularized basis functions. By integrating out the basis coefficients, an implicit copula process on the covariate space is obtained, which we call a `regression copula'. We combine this with a non-parametric margin to define a copula model, where the entire distribution - including the mean and variance - of the response is a smooth semi-parametric function of the covariates. The copula is estimated using both Hamiltonian Monte Carlo and variational Bayes; the latter of which is scalable to high dimensions. Using real data examples and a simulation study we illustrate the efficacy of these estimators and the copula model. In a substantive example, we estimate the distribution of half-hourly electricity spot prices as a function of demand and two time covariates using radial bases and horseshoe regularization. The copula model produces distributional estimates that are locally adaptive with respect to the covariates, and predictions that are more accurate than those from benchmark models.

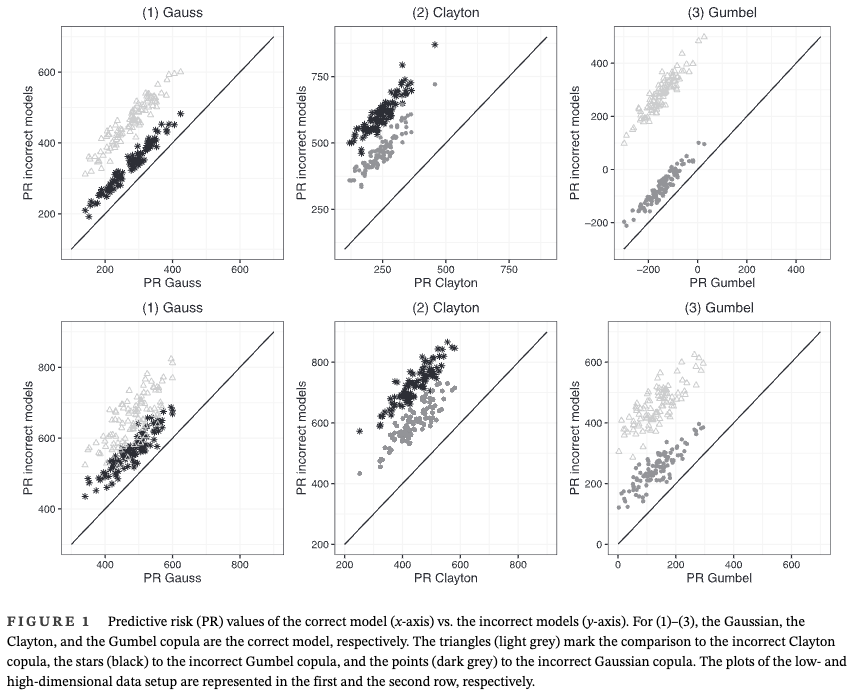
Abstract: Capturing complex dependence structures between outcome variables (e.g., study endpoints) is of high relevance in contemporary biomedical data problems and medical research. Distributional copula regression provides a flexible tool to model the joint distribution of multiple outcome variables by disentangling the marginal response distributions and their dependence structure. In a regression setup, each parameter of the copula model, that is, the marginal distribution parameters and the copula dependence parameters, can be related to covariates via structured additive predictors. We propose a framework to fit distributional copula regression via model-based boosting, which is a modern estimation technique that incorporates useful features like an intrinsic variable selection mechanism, parameter shrinkage and the capability to fit regression models in high-dimensional data setting, that is, situations with more covariates than observations. Thus, model-based boosting does not only complement existing Bayesian and maximum-likelihood based estimation frameworks for this model class but rather enables unique intrinsic mechanisms that can be helpful in many applied problems. The performance of our boosting algorithm for copula regression models with continuous margins is evaluated in simulation studies that cover low- and high-dimensional data settings and situations with and without dependence between the responses. Moreover, distributional copula boosting is used to jointly analyze and predict the length and the weight of newborns conditional on sonographic measurements of the fetus before delivery together with other clinical variables.
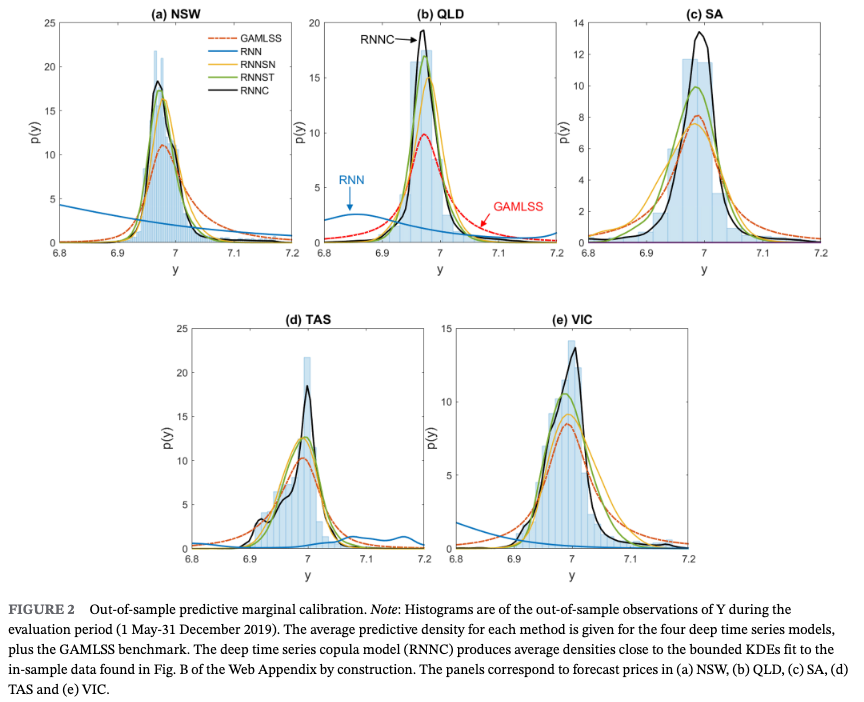
Abstract: Recurrent neural networks (RNNs) with rich feature vectors of past values can provide accurate point forecasts for series that exhibit complex serial dependence. We propose two approaches to constructing deep time series probabilistic models based on a variant of RNN called an echo state network (ESN). The first is where the output layer of the ESN has stochastic disturbances and a Bayesian prior for regularization. The second employs the implicit copula of an ESN with Gaussian disturbances, which is a Gaussian copula process on the feature space. Combining this copula process with a nonparametrically estimated marginal distribution produces a distributional time series model. The resulting probabilistic forecasts are deep functions of the feature vector and marginally calibrated. In both approaches, Markov chain Monte Carlo methods are used to estimate the models and compute forecasts. The proposed models are suitable for the complex task of forecasting intraday electricity prices. Using data from the Australian market, we show that our deep time series models provide accurate short-term probabilistic price forecasts, with the copula model dominating. Moreover, the models provide a flexible framework for incorporating probabilistic forecasts of electricity demand, which increases upper tail forecast accuracy from the copula model significantly.
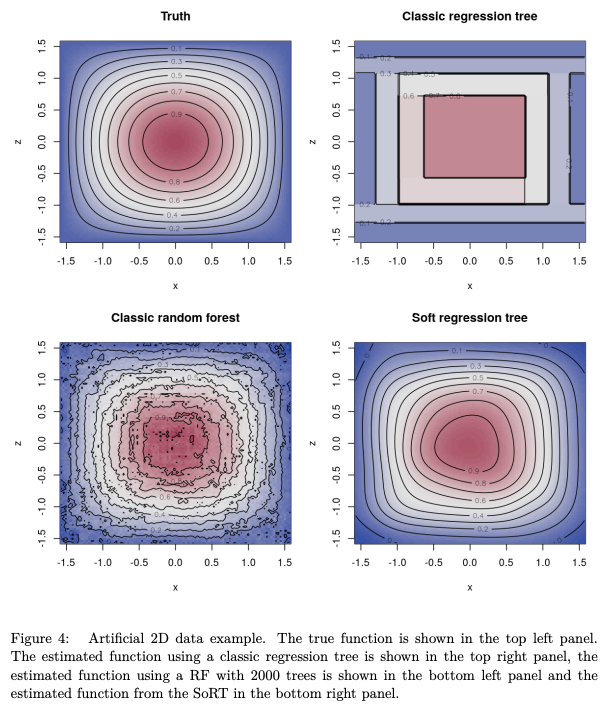
Abstract: Random forests are an ensemble method relevant for many problems, such as regression or classification. They are popular due to their good predictive performance (compared to, e.g., decision trees) requiring only minimal tuning of hyperparameters. They are built via aggregation of multiple regression trees during training and are usually calculated recursively using hard splitting rules. Recently regression forests have been incorporated into the framework of distributional regression, a nowadays popular regression approach aiming at estimating complete conditional distributions rather than relating the mean of an output variable to input features only - as done classically. This article proposes a new type of a distributional regression tree using a multivariate soft split rule. One great advantage of the soft split is that smooth high-dimensional functions can be estimated with only one tree while the complexity of the function is controlled adaptive by information criteria. Moreover, the search for the optimal split variable is obsolete. We show by means of extensive simulation studies that the algorithm has excellent properties and outperforms various benchmark methods, especially in the presence of complex non-linear feature interactions. Finally, we illustrate the usefulness of our approach with an example on probabilistic forecasts for the Sun's activity.
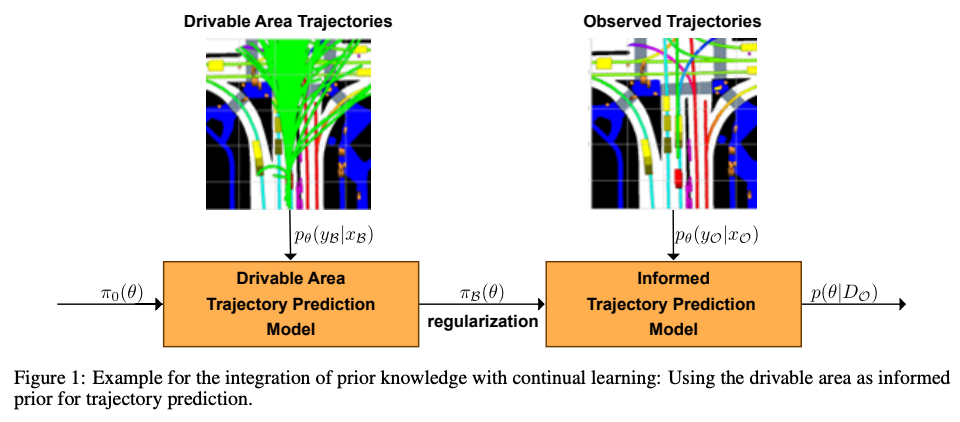
Abstract: Informed learning approaches explicitly integrate prior knowledge into learning systems, which can reduce data needs and increase robustness. However, existing work typically aims to integrate formal scientific knowledge by directly pruning the problem space, which is infeasible for more intuitive world and expert knowledge, or requires specific architecture changes and knowledge representations. We propose a probabilistic informed learning approach to integrate prior world and expert knowledge without these requirements. Our approach repurposes continual learning methods to operationalize Baye’s rule for informed learning and to enable probabilistic and multi-modal predictions. We exemplify our proposal in an application to two state-of-the-art trajectory predictors for autonomous driving. This safety-critical domain is subject to an overwhelming variety of rare scenarios requiring robust and accurate predictions. We evaluate our models on a public benchmark dataset and demonstrate that our approach outperforms non-informed and informed learning baselines. Notably, we can compete with a conventional baseline, even using only half as many observations of the training dataset.
Abstract: Deep neural network (DNN) regression models are widely used in applications requiring state-of-the-art predictive accuracy. However, until recently there has been little work on accurate uncertainty quantification for predictions from such models. We add to this literature by outlining an approach to constructing predictive distributions that are `marginally calibrated'. This is where the long run average of the predictive distributions of the response variable matches the observed empirical margin. Our approach considers a DNN regression with a conditionally Gaussian prior for the final layer weights, from which an implicit copula process on the feature space is extracted. This copula process is combined with a non-parametrically estimated marginal distribution for the response. The end result is a scalable distributional DNN regression method with marginally calibrated predictions, and our work complements existing methods for probability calibration. The approach is first illustrated using two applications of dense layer feed-forward neural networks. However, our main motivating applications are in likelihood-free inference, where distributional deep regression is used to estimate marginal posterior distributions. In two complex ecological time series examples we employ the implicit copulas of convolutional networks, and show that marginal calibration results in improved uncertainty quantification. Our approach also avoids the need for manual specification of summary statistics, a requirement that is burdensome for users and typical of competing likelihood-free inference methods.
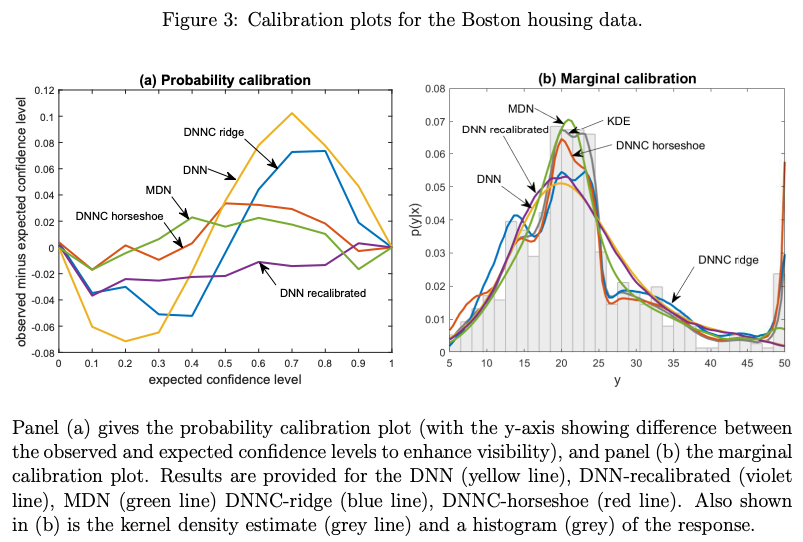
Abstract: End-to-end learners for autonomous driving are deep neural networks that predict the instantaneous steering angle directly from images of the street ahead. These learners must provide reliable uncertainty estimates for their predictions in order to meet safety requirements and to initiate a switch to manual control in areas of high uncertainty. However, end-to-end learners typically only deliver point predictions, since distributional predictions are associated with large increases in training time or additional computational resources during prediction. To address this shortcoming, we investigate efficient and scalable approximate inference for the deep distributional model of Klein, Nott and Smith (J. Comput. Graph. Statist. 30 (2021) 467–483) in order to quantify uncertainty for the predictions of end-to-end learners. A special merit of this model, which we refer to as implicit copula neural linear model (IC-NLM), is that it produces densities for the steering angle that are marginally calibrated, that is, the average of the estimated densities equals the empirical distribution of steering angles. To ensure the scalability to large n regimes, we develop efficient estimation based on variational inference as a fast alternative to computationally intensive, exact inference via Hamiltonian Monte Carlo. We demonstrate the accuracy and speed of the variational approach on two end-to-end learners trained for highway driving using the comma2k19 dataset. The IC-NLM is competitive with other established uncertainty quantification methods for end-to-end learning in terms of nonprobabilistic predictive performance and outperforms them in terms of marginal calibration for in-distribution prediction. Our proposed approach also allows the identification of overconfident learners and contributes to the explainability of black-box end-to-end learners by using the predictive densities to understand which steering actions the learner sees as valid.
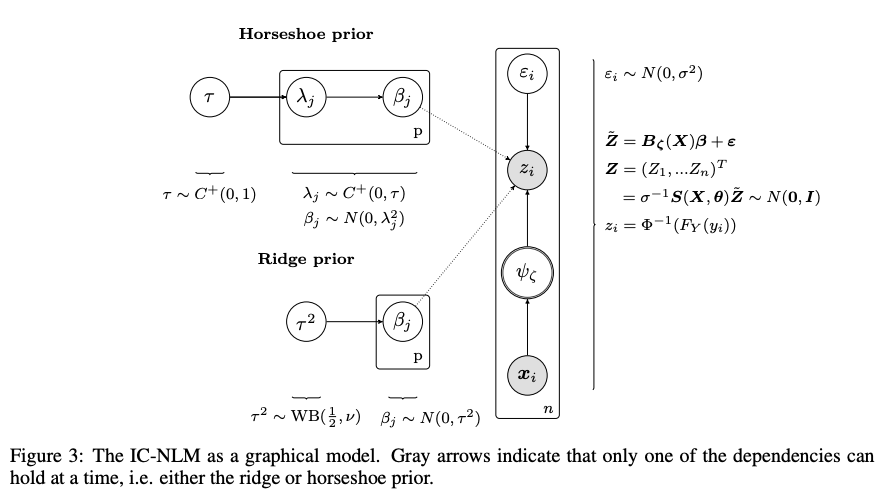
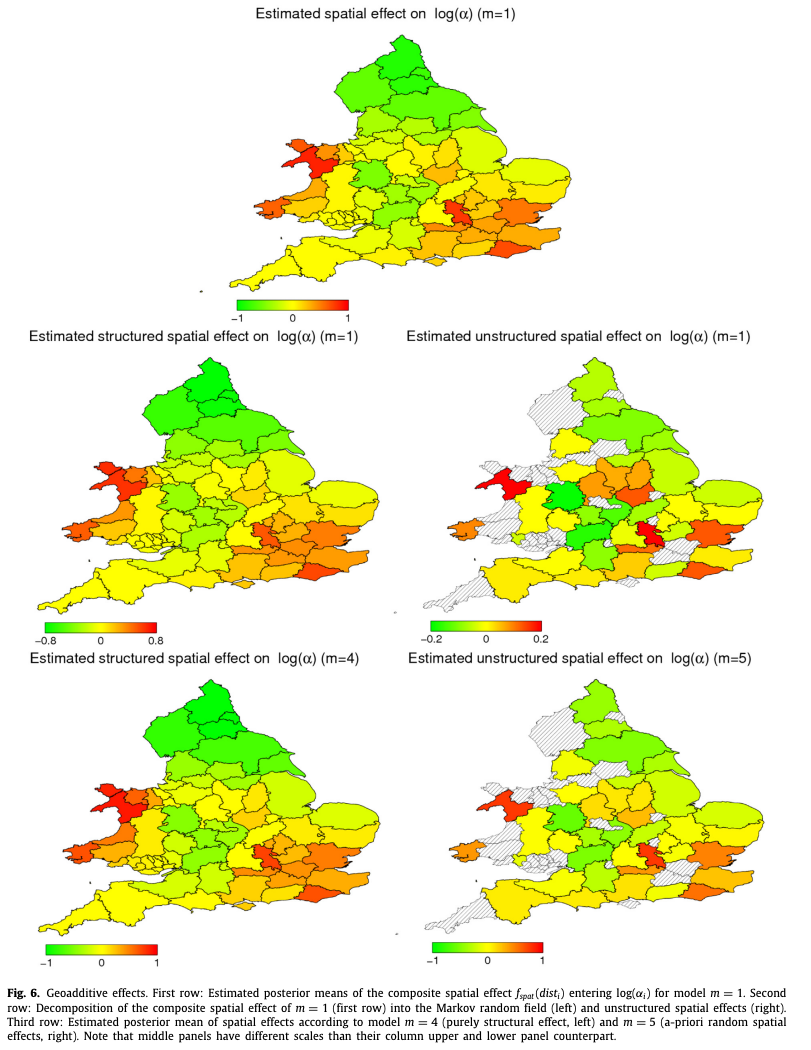
Abstract: We propose a flexible Bayesian approach to inefficiency modelling that accounts for regional patterns of local performance. The model allows for a separated treatment of individual heterogeneity and determinants of inefficiency. Regional dependence structures and location-specific unobserved spatial heterogeneity are modelled via geoadditive predictors in the inefficiency term of the stochastic frontier model. Inference becomes feasible through Markov chain Monte Carlo simulation techniques. In an empirical illustration we find that regional patterns of inefficiency characterize cereal production in England and Wales. Neglecting common performance patterns of farms located in the same region induces systematic biases to inefficiency estimates.
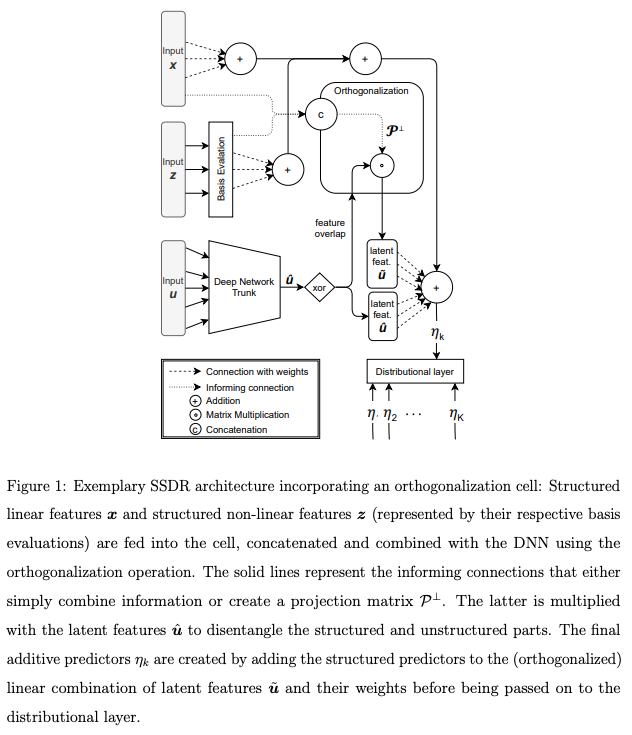
Abstract: Combining additive models and neural networks allows to broaden the scope of statistical regression and extend deep learning-based approaches by interpretable structured additive predictors at the same time. Existing attempts uniting the two modeling approaches are, however, limited to very specific combinations and, more importantly, involve an identifiability issue. As a consequence, interpretability and stable estimation are typically lost. We propose a general framework to combine structured regression models and deep neural networks into a unifying network architecture. To overcome the inherent identifiability issues between different model parts, we construct an orthogonalization cell that projects the deep neural network into the orthogonal complement of the statistical model predictor. This enables proper estimation of structured model parts and thereby interpretability. We demonstrate the framework’s efficacy in numerical experiments and illustrate its special merits in benchmarks and real-world applications.
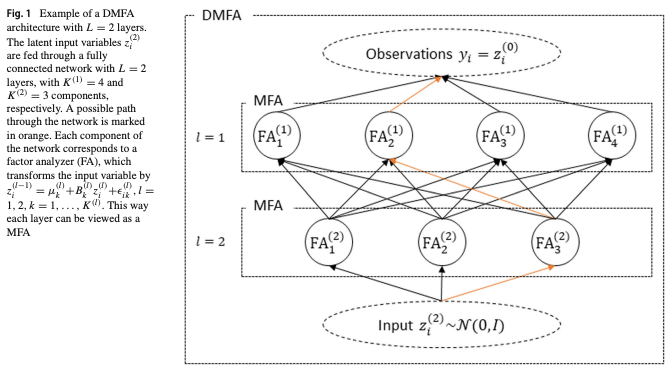
Abstract: Gaussian mixture models are a popular tool for model-based clustering, and mixtures of factor analyzers are Gaussian mixture models having parsimonious factor covariance structure for mixture components. There are several recent extensions of mixture of factor analyzers to deep mixtures, where the Gaussian model for the latent factors is replaced by a mixture of factor analyzers. This construction can be iterated to obtain a model with many layers. These deep models are challenging to fit, and we consider Bayesian inference using sparsity priors to further regularize the estimation. A scalable natural gradient variational inference algorithm is developed for fitting the model, and we suggest computationally efficient approaches to the architecture choice using overfitted mixtures where unnecessary components drop out in the estimation. In a number of simulated and two real examples, we demonstrate the versatility of our approach for high-dimensional problems, and demonstrate that the use of sparsity inducing priors can be helpful for obtaining improved clustering results.