KleinLab - Homepage

Truly Multivariate Structured Additive Distributional Regression

By Lucas Kock and Nadja Klein, posted on April 11, 2025

What is the paper about?

Our paper introduces a novel multivariate distributional regression model that extends generalized additive models for location, scale, and shape (GAMLSS) to truly multivariate responses [1]. This allows for the joint modeling of response vectors with dimensions greater than two or three, including the modeling of the dependence structure. The model relies on a Gaussian copula combined with arbitrary parametric distributions for the marginal responses. Traditional distributional regression models have been limited through fixed dependence structures not depending on covariate, or computational challenges when handling higher-dimensional data. By leveraging Bayesian inference and advances in distributional copula regression our approach overcomes these limitations.

Motivation

The need to analyze complex multivariate data in fields like epidemiology, environmental science, and economics, where responses are not just univariate or bivariate, is increasing. In theory, distributional regression [2] gives a flexible framework to analyse these data sets. However, existing methods often assume simplistic parametric forms for all responses or restrict the dependence structure to be independent of covariates. Our model fills this gap by enabling flexible, covariate-dependent modeling of both the marginal distributions and the dependencies between them.

Theory

Our approach builds on the structured additive distributional regression framework [3] and employs Gaussian copulas [4] for modeling dependencies. Practitioners can specify different parametric forms for each marginal distribution, which allows them to consider mixed responses where some responses may be discrete and others continuous or of mixed type. In addition, the pairwise correlations between response components can vary with covariates. The model is highly parameterized, but the use of Bayesian inference and efficient sampling techniques makes estimation feasible.

Experiments

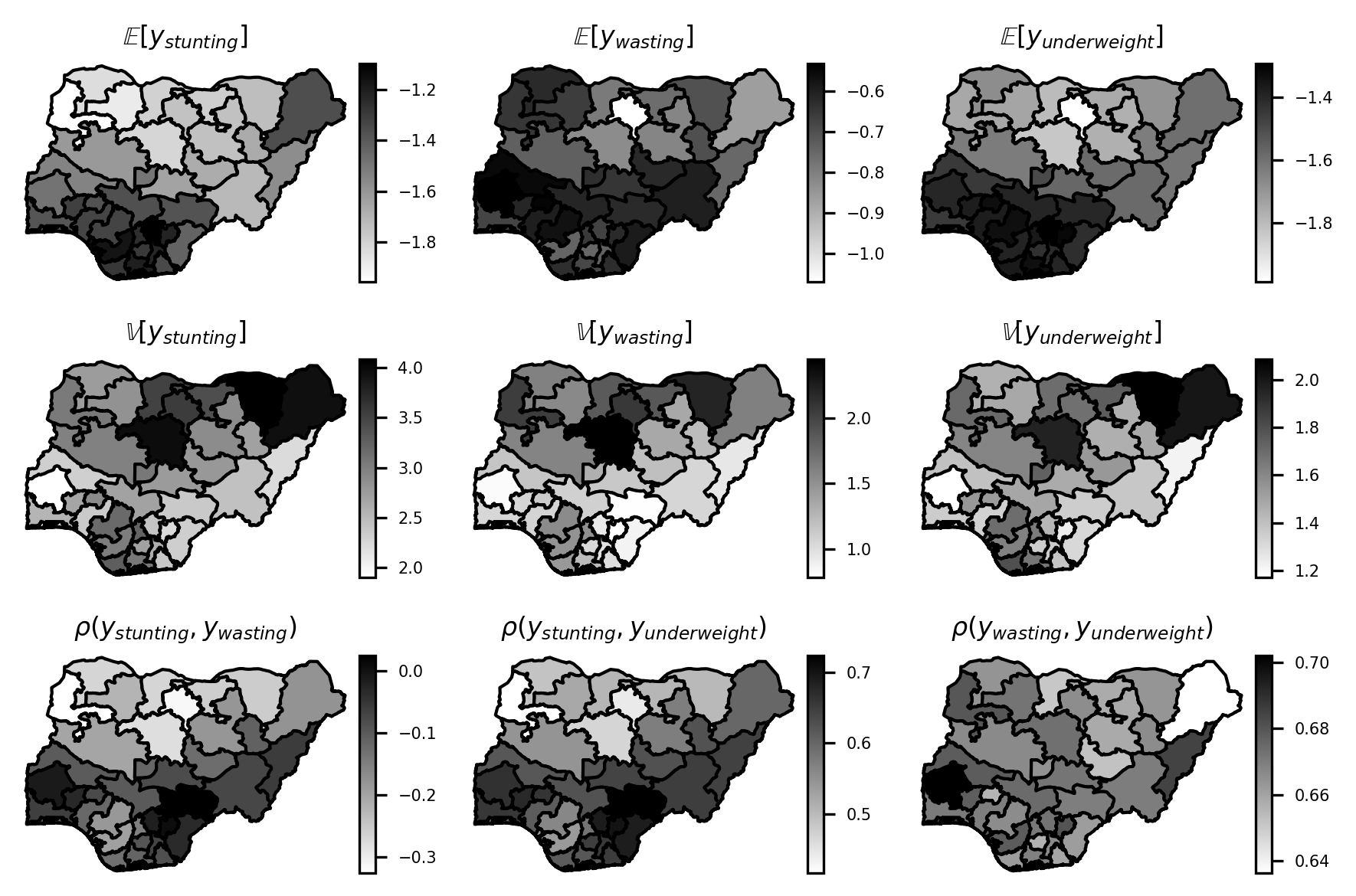
We validated our model using both simulations and real-world datasets. In our simulations, we tested the model's ability to accurately estimate parameters in both Gaussian and non-Gaussian settings, demonstrating flexibility and robustness across various response dimensions even under model missspecificaion. Our real-world applications included studying childhood malnutrition in Nigeria and traffic detection in Berlin.
For childhood malnutrition, we examined three nutritional indicators in Nigerian children, namely stunting, wasting, and underweight referring to insufficient height for age, insufficient weight for height, and insufficient weight for age, respectively, thereby reflecting the different dimensions of childhood undernutrition. Our analysis reveals significant spatial and covariate-driven patterns in nutritional deficiencies. For example, we can visually inspect the influence of the 37 districts in Nigeria jointly on all pairwise correlations as shown in the Figure below.

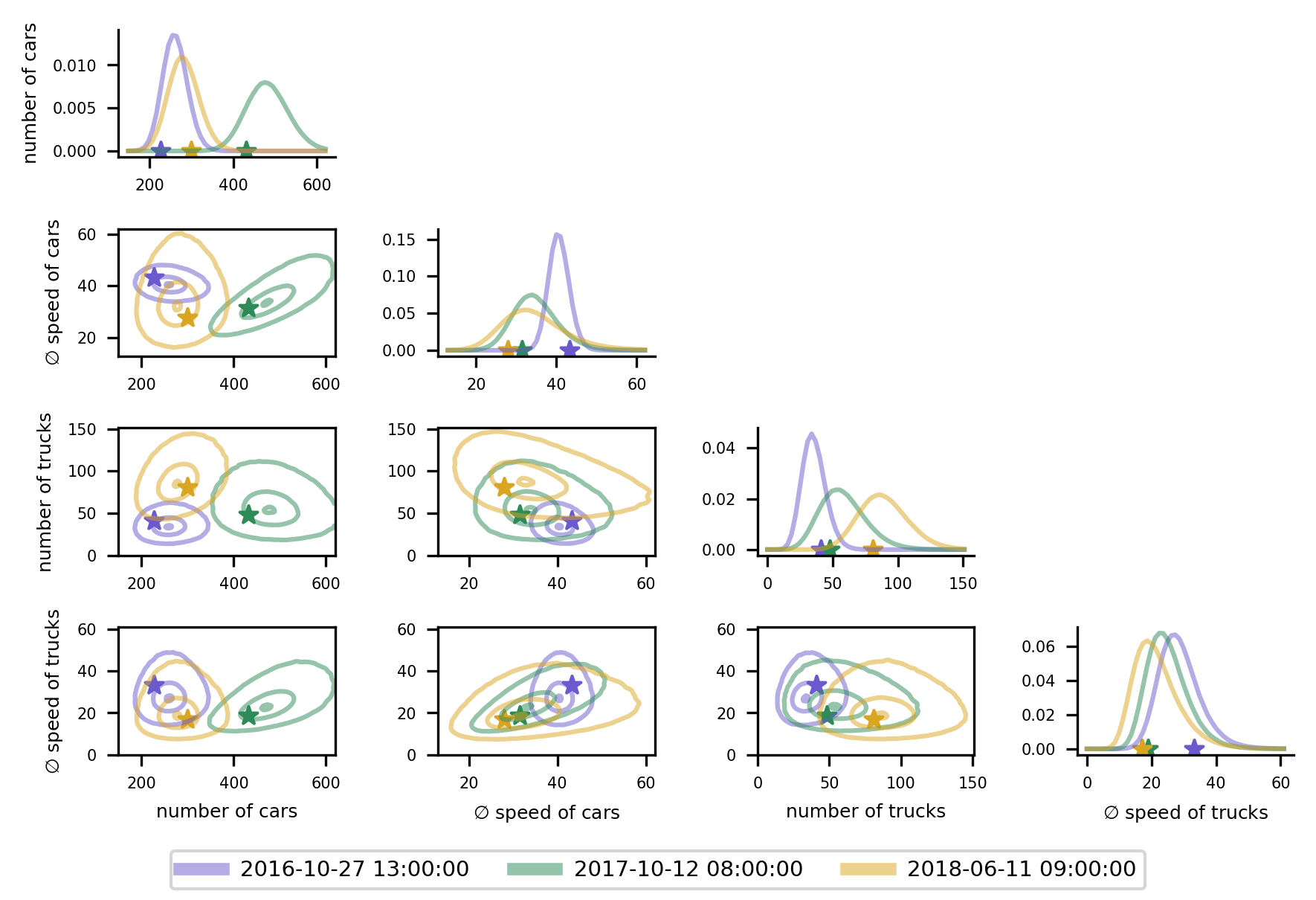
In the Berlin traffic study, we modeled the complex interactions between traffic counts and speeds for cars and trucks over time, offering insights into urban traffic dynamics. The figure below shows univariate marginal densities (diagonal) and bivariate margins (lower left) for three different timepoints, illustrating the high flexibility of the fitted model.

Final Thoughts

Our multivariate distributional regression model provides a powerful tool for researchers needing to explore complex multivariate regression data. By allowing different marginal distributions and covariate-dependent dependencies, it offers a comprehensive approach to understanding intricate regression data structures. We encourage interested readers to explore our work and consider its potential applications in their fields of study.

References

[1] Kock L., Klein N. (2025). Truly multivariate structured additive regression. Journal of Computational and Graphical Statistics; in print, doi: 10.1080/10618600.2024.2434181
[2] Klein N. (2024). Distributional regression for data analysis. Annual Review of Statistics and its Application; 11: 321–346.
[3] Rigby R.A., Stasinopoulos D.M. (2005). Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society, Series C: Applied Statistics; 54: 507–554.
[4] Song P. X.-K., Li M., Yuan Y. (2009). Joint regression analysis of correlated data using Gaussian copulas. Biometrics; 65 (1), 60–68.

For questions, comments or other matters related to this blog post, please contact us via kleinlab@scc.kit.edu.

If you find our work useful, please cite our paper:

@article{KocKle2025, title={Truly Multivariate Structured Additive Distributional Regression}, author={Kock, Lucas and Klein, Nadja}, booktitle={Journal of Computational and Graphical Statistics}, volume={0}, number={0}, pages={1--13}, year={2025}, publisher={ASA Website}, doi={10.1080/10618600.2024.2434181}, }