KleinLab - Homepage

Posterior Concentration Rates for Bayesian Penalized Splines

By Paul Bach and Nadja Klein, posted on May 05, 2025

This blog post is about our paper “Posterior Concentration Rates for Bayesian Penalized Splines” to be published in Bayesian Analysis.You can access the full text here.

What is the paper about?

Bayesian penalized splines (BPS) are highly popular in applied regression modeling. The key idea of the approach is to expand the unknown function to be estimated in a rich spline basis with many knots and to place a smoothness prior on the coefficients to prevent overfitting. The overall amount of regularization is controlled in a data-driven way through a hyperprior on the smoothing variance. This paper investigates the asymptotic properties of BPS and provides the first theoretical guarantees in the literature ensuring optimal asymptotic performance.

Motivation

Since their introduction in the early 2000’s by [1] and [2], BPS have been applied in numerous settings ranging from generalized additive models over additive survival analyses to structured additive distributional regression models. However, despite their widespread use in practice, the asymptotic properties of BPS have not been investigated so far. In this paper, we make an important step to close this gap in the literature and study posterior concentration rates for BPS in a nonparametric regression model. Doing so, we contribute to a better theoretical understanding of BPS.

Theory

To show that the BPS posterior contracts around the unknown function at near optimal rate, we use the Kullback-Leibler (KL) and testing strategy. This is a well-established proof strategy where one needs to verify two conditions [3]. To verify the KL condition we adapt an inequality for a shifted ball under a Gaussian measure and to verify the testing condition, we introduce a completely new test. This test is based on an estimator that projects the observations onto the first basis functions of a Demmler-Reinsch basis. Our results show that BPS can achieve posterior concentration at near optimal rate. However, BPS are not rate-adaptive. This is because the order of the roughness penalty in the smoothness prior needs to match the regularity of the unknown function exactly to achieve the optimal rate of concentration.

Experiments

We conduct a simulation study to judge the empirical performance of BPS in comparison with other nonparametric regression methods. To this end, we benchmark BPS against Gaussian processes with a squared exponential kernel as well as Bayesian splines with a hyperprior on the number of knots. The latter approach is a close relative of BPS and has been shown to yield rate-adaptive posterior concentration [4]. Overall, we find that that BPS provide competitive performance with a slight advantage over Gaussian processes and a slight disadvantage compared to Bayesian splines with a hyperprior on the number of knots.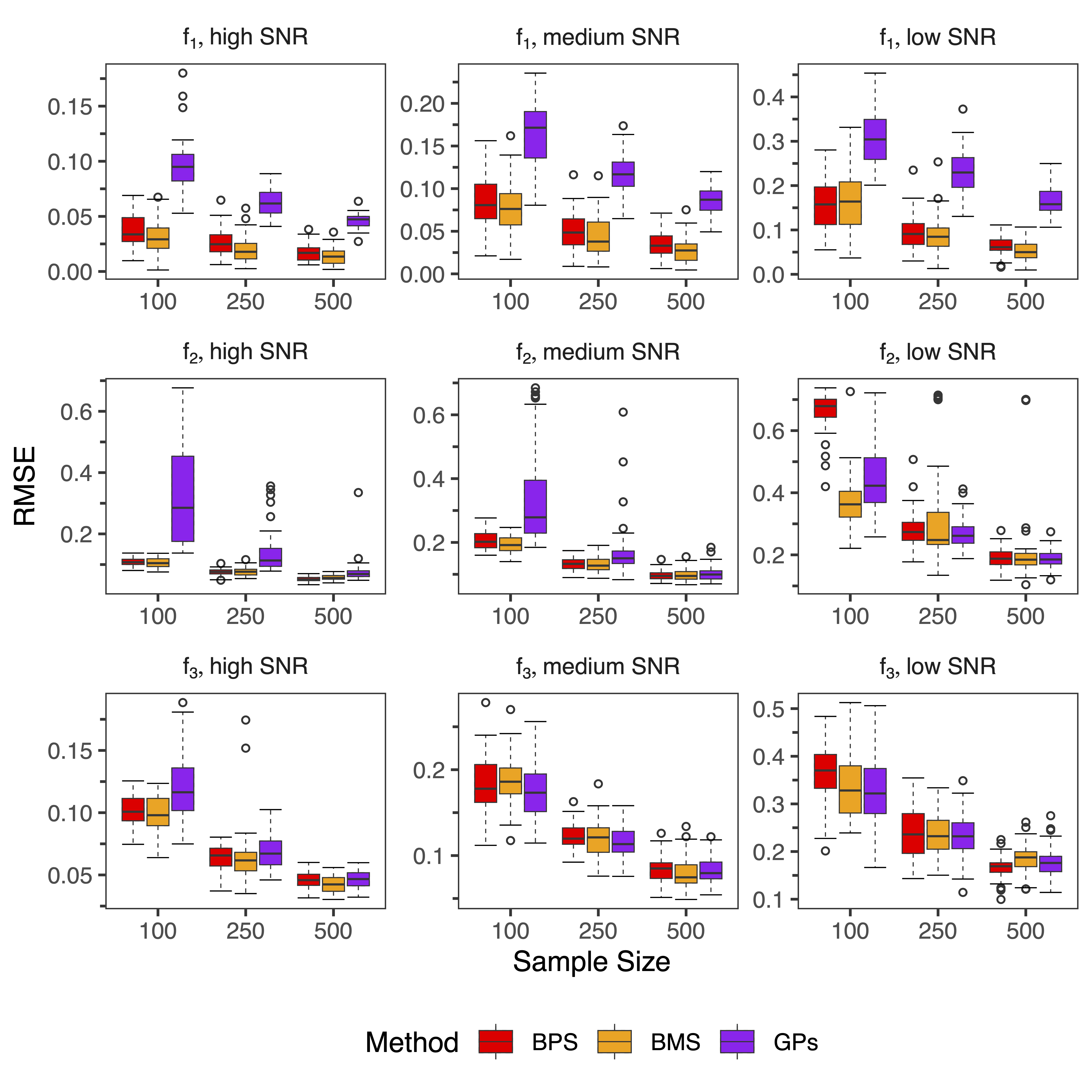

Figure 1: Root mean squared error (RMSE) of Bayesian penalized splines (BPS), Bayesian splines with a hyperprior on the number of knots (BMS) and Gaussian processes (GPs). Lower is better.

Final Thoughts

It is an interesting finding that BPS can achieve the optimal rate but that they are not rate-adaptive. From a theoretical perspective, BPS are thus actually inferior to Bayesian splines with a hyperprior on the number of knots. However, it is much easier to set up a Markov chain Monte Carlo sampler for BPS, which has contributed to their immense popularity. In conclusion, we see several promising directions for future research, which you can find in the final section of our paper.

References

[1] Berry, S. M., Carroll, R. J., Ruppert, D. (2002). Bayesian smoothing and regression splines for measurement error problems. Journal of the American Statistical Association; 97(457): 160-169.
[2] Lang, S., Brezger, A. (2004). Bayesian P-splines. Journal of Computational and Graphical Statistics; 13(1): 183-212.
[3] Ghosal, S., Van der Vaart, A. W. (2017). Fundamentals of Nonparametric Bayesian Inference. Cambridge University Press, Cambridge, UK.
[4] de Jonge, R., van Zanten, J.H. (2012). Adaptive estimation of multivariate functions using conditionally Gaussian tensor-product spline priors. Electronic Journal of Statistics; 6: 1984-2001.

For questions, comments or other matters related to this blog post, please contact us via kleinlab@scc.kit.edu.

If you find our work useful, please cite our paper:

@inproceedings{BacKle2025, author={Paul Bach and Nadja Klein}, title={Posterior Concentration Rates for Bayesian Penalized Splines}, journal={Bayesian Analysis}, publisher={International Society for Bayesian Analysis}, pages={1--21}, year={2025}, doi={10.1214/25-BA1523}, URL={https://doi.org/10.1214/25-BA1523}, }