KleinLab - Homepage

Modeling Dependent Censoring in Time-to-Event Data using Boosting Copula Regression

By Annika Strömer and Nadja Klein, posted on October 24, 2025

This blog post is about our paper Modeling dependent censoring in time-to-event data using boosting copula regression published in Lifetime Data Analysis and which can be found here.

Figure 1: Graphical illustration of two survival scenarios with right-censoring. In both scenarios, the event and censoring times $ F $ and $ C $ are conditional on the covariates $ X $. Furthermore, $ T $ is the observed survival time, $ \delta $ is the event indicator and $ U $ is an unobserved confounder. The left-hand graph displays independent censoring and the right-hand graph dependent censoring: a) direct dependence from $ T $ to $ C $ and b) indirect dependence through the unmeasured covariate.

What is the paper about?

The paper introduces a statistical boosting algorithm for modeling dependent censoring in time-to-event data using copula regression. The proposed method provides a flexible, data-driven approach to account for situations in which censoring is not independent of the event of interest, a phenomenon frequently encountered in practice.

Motivation

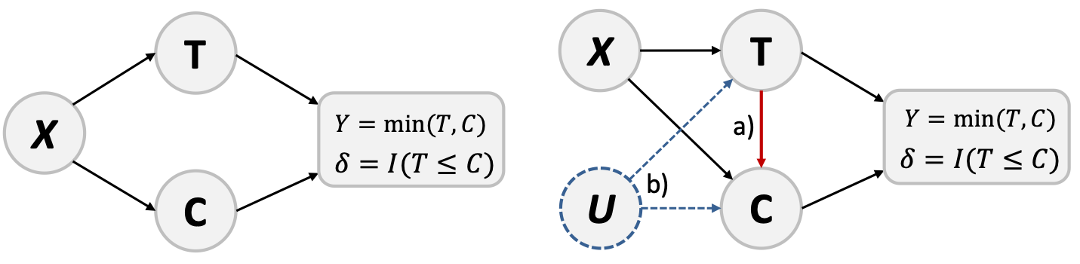
Censored observations are a natural feature of survival analysis: some patients do not experience the event of interest (e.g., death, relapse, or recovery) during the study period or they may be lost to follow-up. Traditional methods [1,2] typically assume independent censoring, meaning the censoring time is independent of the event time (see the left part of Figure 1). However, this assumption often does not hold in real-world studies. For example, patients in poor health may be more likely to withdraw from a study, leading to a dependence between their survival and censoring times, as illustrated in the right part of Figure 1. When such dependence exists, classical approaches that assume independence between censoring and survival times can lead to biased results. Our paper addresses this issue by explicitly modeling the dependence between event time $ T $ and censoring time $ C $ using a copula, enabling a more flexible and realistic joint distribution of survival and censoring times.

Theory

Our paper builds on recent work by Czado and Van Keilegom (2023, [3]) and Deresa et al. (2022, [4]). Our method utilizes a parametric copula combined with arbitrary parametric marginal distributions, allowing for a joint distribution function of the survival time $ T $ and censoring time $ C $. In particular, based on Sklar's theorem, we assume $$ F_{(T,C)} (t,c\mid \alpha) = C\{F_T (t\mid \theta_T),F_C (c\mid \theta_C)\mid \theta\} $$ where $ F_T $ and $ F_C $ are the marginal distributions of the survival and censoring times, respectively. The parameter vector $ \alpha = (\theta_T, \theta_C, \theta)^T $ contains all model parameters for the marginals and copula. Each component of $ \alpha $ can be flexibly linked to covariates via additive predictors and suitable link functions.
Estimation is performed using statistical boosting, enabling the simultaneous modeling of all distribution parameters as functions of potentially different sets of covariates. This approach can handle high-dimensional cases where the number of covariates exceeds the number of observations ($ p \gt n $), for which most classical approaches are no longer feasible. Furthermore, the boosting approach has the advantage of including a data-driven variable selection mechanism. This feature is particularly beneficial when dealing with many potential predictors, ensuring that only the most relevant variables are included without compromising predictive power.

Experiments

We conducted an extensive simulation study to evaluate the performance of the proposed method under various dependence structures and censoring mechanisms. The results demonstrate that our approach performs well in both identifying and estimating informative variables across a range of challenging scenarios.
Finally, we illustrated our approach using data from a recent observational oncology study investigating the overall survival of patients with colon cancer. This application highlights the practical advantages of our method. The boosting copula regression framework provides additional insights into the dependence between survival and censoring times that are not captured by classical approaches. Among other findings, we identified a negative effect of chemotherapy on the relationship between survival and censoring, an effect that could not be detected using previous models.

Final Thoughts

Dependent censoring is frequently overlooked in survival analysis but can meaningfully influence results. Our framework offers a flexible, data-driven, and interpretable strategy to model this dependence, uncovering new relationships in biomedical research. We hope these advances encourage researchers to account for dependence structures in time-to-event analyses and to explore the benefits of boosting and copula-based modeling in practice.

References

[1] Cox D. R. (1972). Regression models and life-tables. Journal of the Royal Statistical Society: Series B (Methodological), 34(2):187-202.
[2] Kaplan E. L. And Meier P. (1958). Nonparametric estimation from incomplete observations. Journal of the American Statistical Association, 53(282):457-481.
[3] Czado C. and Van Keilegom I. (2023). Dependent censoring based on parametric copulas. Biometrika, 110(3):721-738.
[4] Deresa N. W., Van Keilegom I. and Antonio K. (2022). Copula-based inference for bivariate survival data with left truncation and dependent censoring. Mathematics and Economics, 107:1-21.

For questions, comments or other matters related to this blog post, please contact us via kleinlab@scc.kit.edu.

If you find our work useful, please cite our paper:

@inproceedings{StrKleVanMay2025, title={Modelling dependent censoring in time-to-event data using boosting copula regression}, author={Str{\"o}mer, Annika and Klein, Nadja and {Van Keilegom}, Ingrid and Mayr, Andreas}, year={2025}, journal={Lifetime Data Analysis}, doi={10.1007/s10985-025-09674-x}, URL={https://doi.org/10.1007/s10985-025-09674-x} isbn={1572-9249} }