KleinLab - Homepage

Boosting distributional copula regression for bivariate binary, discrete and mixed responses

By Guillermo Briseño Sanchez and Nadja Klein, posted on April 01, 2025

This blog post is about our paper “Boosting distributional regression for bivariate binary, discrete and mixed responses” which was published in Statistical Methods in Medical Research, and which can be found here. The accompanying code and data are available on GitHub.

What is the paper about?

The article presents a statistical boosting algorithm tailored for bivariate distributional copula regression. Compared to Hans et. al (2023, [1]), our method cannot only deal with continuous outcomes but also binary, count, or mixed responses.
Using our framework, practitioners can specify suitable distributions for the marginal response variables. A flexible joint bivariate distribution is then constructed using a copula function, which links the two marginal responses and induces a dependence structure to be learned from the data. To handle high-dimensional covariates or feature variables, we estimate the both the marginal distributions and the dependence structure jointly using component-wise gradient boosting.

Figure 1: Responses in the biomedical applications analysed in Section 4 of the paper: (a) binary–binary response (numbers indicate proportions): high cholesterol and chronic ischemic heart disease; (b) count–count response (numbers indicate cases): doctor visits and medical prescriptions; and (c) binary–continuous response: fever and wasting (indicator for acute undernutrition)

Motivation

Distributional regression models [2] have gained popularity in statistical research by allowing to model the entire conditional distribution of a response variable as a function of covariates, rather than just its conditional mean, as done in traditional regression. Distributional models are also useful in biomedical research, as they help explore how variables affect not just the average of the quantities of interest but also other aspects like their variances or certain quantiles.
This paper builds on an approach known as generalized additive models for location, scale, and shape (GAMLSS [3]). In this statistical framework, potentially all parameters of the response distribution can be related to covariates.
In biomedical applications, the outcomes of interest may have dependent components that are are not continuous but instead binary (disease yes / no), discrete (number of doctor consultations) or of mixed type.

Theory

Our paper builds on recent work by Hans, et al. (2023, [1]), who developed component-wise gradient boosting for bivariate distributional copula regression with continuous response variables. We use the same idea and model the bivariate distribution of two responses $y_1, y_2$ as $$ F(y_1, y_2) = C[F_1(y_1), F_2(y_2), \vartheta ] $$ As shown in the equation above, the copula approach requires the marginal distributions $ F_1(y_1) $ and $ F_2(y_2) $, whereas the dependence structure between the variables is determined by the copula with dependence parameter $ \vartheta$.
Every parameter of the marginal distributions as well as the dependence parameter $ \vartheta$ can be modelled as a function of the explanatory variables.
To handle high-dimensional biomedical data, we resort to estimating the model using component-wise boosting and we provide an implementation as part of the R package gamboostLSS [4].

Experiments

We demonstrate the flexibility of the proposed boosted distributional copula regression approach by analysing three biomedical research questions, related to chronic ischemic heart disease and high-cholesterol (bivariate binary), the number of doctor consultations and prescribed medications (bivariate count), and infant undernutrition in India (mixed binary-continuous).
We briefly illustrate our method along two of our applications. The first study has two bivariate binary responses, which are chronic ischemic heart disease (yes/no) and high-cholesterol (yes/no). In this application, the explanatory variables indicate gene expressions associated with the individuals in the study. The data is from the UK Biobank [5] and includes a high-dimensional feature information (p=1867 explanatory variables) from n=30,000 individuals. Our method selects several genetic variants in the parameters of the bivariate distribution. The Manhattan-type plot below shows the chromosome location of the genetic variants selected.

Figure 2: Manhattan-type plots of the estimated coefficients (expressed in exponential absolute values of the estimated values) of the boosted bivariate binary model using a Gaussian copula. The x-axis represents the genomic location of the variants and the y-axis shows $\exp( | \hat{ \beta_j } | ), j = 1, ..., p$.

The second application is on childhood undernutrition in India using the data from [6]. We analysed the joint distribution of a binary variable (fever yes/no before survey interview) and a malnutrition indicator (wasting; low weight for height), which measures acute undernutrition. The figure below shows the estimated dependence between these outcomes expressed as Kendall’s tau and averaged by administrative area:

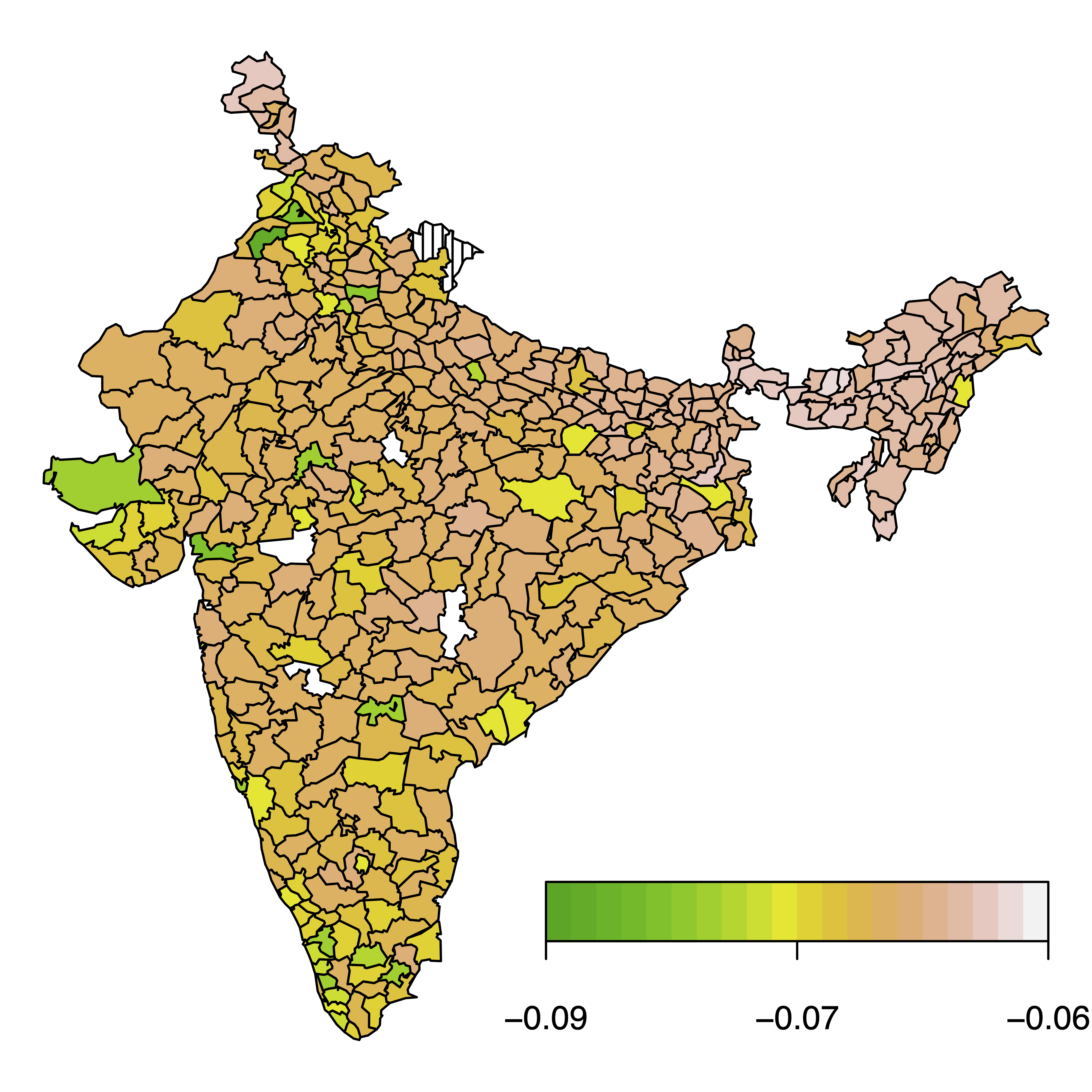
Figure 3: Estimated Kendall’s $\tau$ of having fever and acute undernutrition averaged by administrative areas according to the Clayton copula rotated by 270°.

One can see that dependence between the fever indicator and wasting changes according to the administrative areas of India, with slightly stronger negative dependence between the marginal variables in the west of the country. Our results agree with previous analyses of Klein, et. al (2019, [6]), but with the added benefit of variable selection being conducted automatically by our estimation algorithm.

Final Thoughts

Our approach can be a helpful tool to analyse biomedical data with potentially high-dimensional explanatory variables. The use of component-wise boosting allows for data-driven variable selection.

References

[1] Hans N., Klein N., Faschingbauer F., et al. (2023). Boosting distributional copula regression. Biometrics; 79: 2298–2310.
[2] Klein N. (2024). Distributional regression for data analysis. Annual Review of Statistics and its Application; 11: 321–346.
[3] Rigby R.A., Stasinopoulos D.M. (2005). Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society, Series C: Applied Statistics; 54: 507–554.
[4] Hofner B., Mayr A., Schmid M. (2016). gamboostLSS: An R package for model building and variable selection in the GAMLSS framework. Journal of Statistical Software; 74: 1–31.
[5] Bycroft C, Freeman C, Petkova D, et al. (2018). The UK Biobank resource with deep phenotyping and genomic data. Nature; 562: 203–209.
[6] Klein N., Kneib T., Marra G., et al. (2019). Mixed binary-continuous copula regression models with application to adverse birth outcomes. Statistics in Medicine; 38: 413–436.

For questions, comments or other matters related to this blog post, please contact us via kleinlab@scc.kit.edu.

If you find our work useful, please cite our paper:

@inproceedings{BriKleKliMay2025, title={Boosting distributional copula regression for bivariate binary, discrete and mixed responses}, ISSN={1477-0334}, url={http://dx.doi.org/10.1177/09622802241313294}, DOI={10.1177/09622802241313294}, journal={Statistical Methods in Medical Research}, publisher={SAGE Publications}, author={Guillermo {Brise\~no Sanchez} and Nadja Klein and Hannah Klinkhammer and Andreas Mayr}, year={2025}, month=mar }