KleinLab - Homepage

Boosting Causal Additive Models

By Maximilian Kertel and Nadja Klein, posted on September 13, 2025

This blog posts presents our paper “Boosting Causal Additive Models”, which was published in the Journal of Machine Learning Research (JMLR). The paper can be found here and the code is available here.

What is the paper about?

This paper introduces a novel method for causal discovery from purely observational data. The research focuses on a class of models known as Causal Additive Models (CAMs), which assume that variables follow a Structural Equation Model (SEM) with additive noise. We present a boosting-based approach that can consistently identify the causal ordering of variables.

Motivation

Finding the underlying causal relationships in complex datasets, such as those found in genetics or manufacturing, is crucial for improving decisions and predictions. The most reliable method, controlled experiments (like Design of Experiments), is often too resource-intensive, or even unethical to perform. The era of Big Data and the Internet of Things (IoT) provides vast amounts of observational data, but deriving causal structures from this data remains a major challenge. Many existing algorithms lack theoretical guarantees and exhibit inconsistent performance across different datasets. Our work fills this gap by proposing a reliable method with theoretical foundations.

Theory

The paper simplifies the problem of finding the causal graph by identifying its topological ordering—a permutation of variables where causes always precede effects. The proposed method works by regressing each variable on its predecessors in each ordering and then evaluating the squared residuals. Proposition 1 outlines two key conditions for any regression technique to consistently find the true causal order:

1. Consistency in a Correct Model: The regression method must be able to accurately identify the true functional relationships when they exist.
2. Robustness to Misspecification: The method must not overfit the data, even when the underlying relationships deviate from the assumed model.

The paper proves that nonparametric L2 boosting with early stopping satisfies both conditions, thus establishing it as a consistent and robust approach for causal discovery. For datasets of high dimensions where a full search for the optimal causal order is computationally infeasible, we propose a greedy, component-wise boosting algorithm.

Figure 1: The blue dots represent 500 realizations of a distribution following a CAM with p = 2 with graph \( X_1 \to X_2 \). In the left-hand plot, \( X_2 \) is shown on the y-axis and \( X_1 \) on the x-axis, while in the right-hand plot, the axes are reversed. The red lines give the conditional mean functions, that is, the optimal L2-regressions. The unexplained noise (distance of blue dots to red line) is smaller in the left plot, which is the correct ordering.

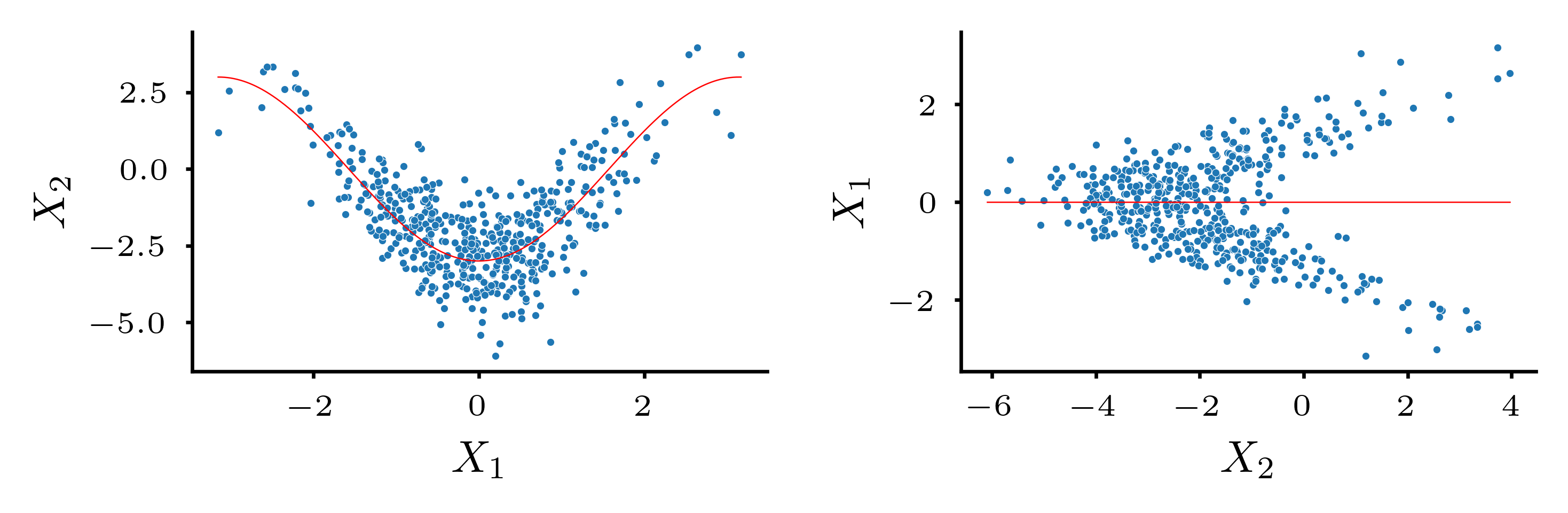
Experiments

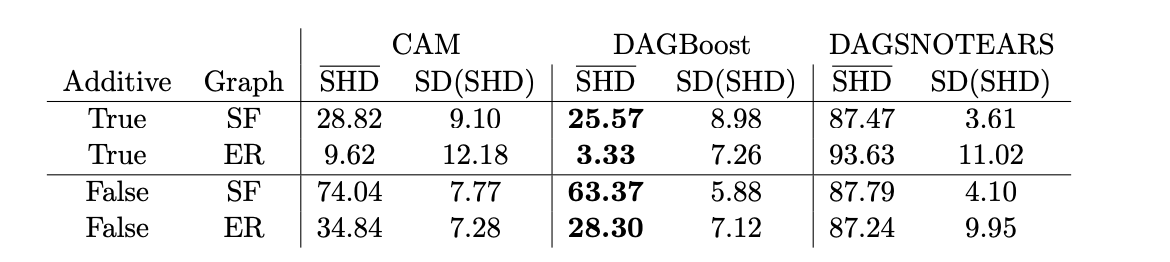
The empirical studies support the theoretical findings in a low-dimensional setting. For a small numbers of variables (p=5), the method quickly converges to the correct causal ordering as the sample size increases. Importantly, this consistency holds even when the data generation process deviates from the model's assumptions, demonstrating its robustness to misspecification.
In high-dimensional settings (p=100), the proposed greedy algorithm, named DAGBoost, was benchmarked against two state-of-the-art methods, CAM [2] and DAGSNOTEARS [3]. DAGBoost and CAM both significantly outperformed DAGSNOTEARS. Across different simulation scenarios, DAGBoost outperformed CAM slightly. While CAM achieved a slightly higher recall (finding more true edges), DAGBoost demonstrated superior precision, meaning that a higher percentage of the edges it identified were correct. This makes DAGBoost particularly valuable in applications, where false positives can lead to significant issues.

Figure 2: Mean and standard deviation of the Structural Hamming Distances (SHDs) between the true graph and the graphs estimated by the three presented algorithms. Erdös-Renyi (ER) graphs have edges evenly distributed among the nodes. Scale-free (SF) graphs have edges unevenly distributed among the nodes, with a small number of nodes having many in- or outgoing edges. We considered data generated by additive functional relationships (matching the CAM) and non-additive relationships (not matching the CAM).

Final Thoughts

Our work not only provides a powerful tool for causal discovery but also offers a theoretical explanation for the well-known empirical success of boosting with early stopping. The proof of boosting's robustness to misspecification is a side-product of the paper and helps explaining its strong performance in real-world scenarios. Further, the general theoretical framework can be applied to other regression techniques, such as neural networks, paving the way for future research in this area.

References

[1] M. Kertel and Klein N. (2025). Boosting Causal Additive Models. Journal of Machine Learning Research; 26: 169.
[2] P. Bühlmann et. al. (2014). Causal Additive Models. The Annals of Statistics; 42 (6) 2526 - 2556.
[3] X. Zheng et. al. (2020). Learning Sparse Nonparametric DAGs. Proceedings of Machine Learning Research; 108:3414-3425.
[4] J. Peters et. al. (2014). Causal Discovery with Continuous Additive Noise Models. Journal of Machine Learning Research; 15:58.

For questions, comments or other matters related to this blog post, please contact us via kleinlab@scc.kit.edu.

If you find our work useful, please cite our paper:

@misc{KerKle2025, author={Maximilian Kertel and Nadja Klein}, title={Boosting Causal Additive Models}, journal={Journal of Machine Learning Research}, year={2025}, volume={26}, number={169}, pages={1--49}, url={http://jmlr.org/papers/v26/24-0052.html}, }